Selección del tipo de Reactor Ideal Diseño de Reactores Químicos
F.Cunill, M.Iborra, J.Tejero

Criterio de óptimo: tiempo espacial mínimo
En el diseño de plantas químicas frecuentemente es necesario determinar que tipo de reactor, ó modelo de contacto, es el adecuado para un sistema reaccionante y unas condiciones de trabajo determinadas. Los factores a considerar son numerosos, tantos que no es posible dar una fórmula directa para responder la pregunta.
Entre los factores a considerar figuran:
En el diseño de plantas químicas frecuentemente es necesario determinar que tipo de reactor, ó modelo de contacto, es el adecuado para un sistema reaccionante y unas condiciones de trabajo determinadas. Los factores a considerar son numerosos, tantos que no es posible dar una fórmula directa para responder la pregunta.
Entre los factores a considerar figuran:
- Tipo de reacción: Reacción única o reacciones múltiples
- Escala de producción. Coste de aparatos, de funcionamiento y vida útil de los aparatos
- Características de operación. Seguridad. Estabilidad. Flexibilidad
- Convertibilidad a otros procesos
Para REACCIONES SIMPLES (una sola expresión cinética describe el curso de la reacción) el criterio es el de máxima productividad ya que no tiene sentido hablar de selectividad. Por tanto, para un volumen de reactor dado se busca la máxima conversión ó producción (caudal x conversión), mientras que para una conversión fijada se busca el mínimo volumen de reacción.
En este capítulo se mostrará que para cada reacción tenemos un modelo de flujo más eficiente, dependiendo del tipo de cinética y de la conversión exigida.
Reactor de flujo en pistón con recirculación. Ecuación de diseño. Razón de recirculación óptima
En determinadas situaciones es interesante dividir la corriente de salida de un reactor de flujo (RFP) en pistón y retornar parte de ella a la entrada del mismo.
Con esta disposición es posible que un RFP globalmente adquiera características de reactor de mezcla perfecta (RMP). Esta situación se presenta con frecuencia en el diseño de reactores catalíticos. Esta opción se utiliza con reacciones autocatalíticas, cuando es necesario mantener la isotermicidad o promover cierta selectividad. Es muy usado en operaciones bioquímicas.
Se define la relación o razón de recirculación, R, como la razón entre el caudal que retorna a la entrada y el que sale del sistema. Puesto que las condiciones físicas de las corrientes 3 y 4 son idénticas se tiene que la razón de recirculación es

La razón de recirculación puede variar de cero a infinito. Intuitivamente puede deducirse que a medida que R aumenta el comportamiento se desvía del flujo en pistón adquiriendo mayores características de mezcla perfecta. Por tanto, la recirculación proporciona un medio para obtener distintos grados de retromezcla en un reactor de flujo en pistón.
Ecuación de diseño
Para evitar incongruencias en la conversión dado que se recircula una corriente con producto, la ecuación de diseño para un reactor de flujo en pistón con recirculación se define en función de unas nuevas variables, w’Ao y X’A, las cuales habrá que especificar en función de las periféricas
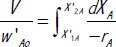
La ecuación anterior es la de diseño de un FP en el que la corriente de entrada està libre de producto. Dicha corriente es w’Ao y es necesario relacionarla con las variables periféricas del sistema. Para ello se define w’Ao como el caudal que entra en el reactor ideal de FP si no hay reacción, es decir, es w1A. Por otro lado si se considera que no hay reacción wAo=w4A y w1A=w2A=w4A+w3A= w4A+ w4AR=(1+R) w4A, de manera que

Las conversiones X’ se definen sobre la anterior variable de forma que
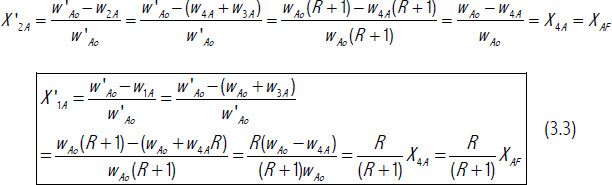
Por tanto, la ecuación de diseño de un RFP con recirculación en función de las variables periféricas es la siguiente

La Figura 3.1 muestra la interpretación gráfica de la ecuación anterior. La integral , es decir, el área bajo la curva entre la conversión a la entrada del reactor
, es decir, el área bajo la curva entre la conversión a la entrada del reactor  y la de salida del reactor XAF, es el área de color verde, cuyo valor es
y la de salida del reactor XAF, es el área de color verde, cuyo valor es  .
.
Por lo tanto, , es el área del rectángulo rayado. El área de la parte azul del rectángulo rayado es R veces el área de la integral I, y el área de la parte gris del rectángulo rayado es equivalente a la integral I. A continuación la Figura 3.2 muestra gráficamente la influencia de la razón de recirculación
, es el área del rectángulo rayado. El área de la parte azul del rectángulo rayado es R veces el área de la integral I, y el área de la parte gris del rectángulo rayado es equivalente a la integral I. A continuación la Figura 3.2 muestra gráficamente la influencia de la razón de recirculación


Si la densidad del medio permanece constante la ecuación de diseño se transforma en
 Razón óptima de recirculación para un volumen mínimo
Razón óptima de recirculación para un volumen mínimo
Al observar la variación grafica que produce la razón de recirculación se deduce que existe una razón óptima para la cual el volumen del reactor es mínimo. Dicha razón óptima depende de la forma de la curva cinética y del grado de conversión a alcanzar.

Ello ocurre cuando las áreas señaladas en la gráfica son iguales. (Demostración matemática Levenspiel, O. Pag 167. Ed Reverté).


En este capítulo se mostrará que para cada reacción tenemos un modelo de flujo más eficiente, dependiendo del tipo de cinética y de la conversión exigida.
Reactor de flujo en pistón con recirculación. Ecuación de diseño. Razón de recirculación óptima
En determinadas situaciones es interesante dividir la corriente de salida de un reactor de flujo (RFP) en pistón y retornar parte de ella a la entrada del mismo.
Con esta disposición es posible que un RFP globalmente adquiera características de reactor de mezcla perfecta (RMP). Esta situación se presenta con frecuencia en el diseño de reactores catalíticos. Esta opción se utiliza con reacciones autocatalíticas, cuando es necesario mantener la isotermicidad o promover cierta selectividad. Es muy usado en operaciones bioquímicas.
Se define la relación o razón de recirculación, R, como la razón entre el caudal que retorna a la entrada y el que sale del sistema. Puesto que las condiciones físicas de las corrientes 3 y 4 son idénticas se tiene que la razón de recirculación es

La razón de recirculación puede variar de cero a infinito. Intuitivamente puede deducirse que a medida que R aumenta el comportamiento se desvía del flujo en pistón adquiriendo mayores características de mezcla perfecta. Por tanto, la recirculación proporciona un medio para obtener distintos grados de retromezcla en un reactor de flujo en pistón.
Ecuación de diseño
Para evitar incongruencias en la conversión dado que se recircula una corriente con producto, la ecuación de diseño para un reactor de flujo en pistón con recirculación se define en función de unas nuevas variables, w’Ao y X’A, las cuales habrá que especificar en función de las periféricas
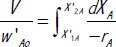
La ecuación anterior es la de diseño de un FP en el que la corriente de entrada està libre de producto. Dicha corriente es w’Ao y es necesario relacionarla con las variables periféricas del sistema. Para ello se define w’Ao como el caudal que entra en el reactor ideal de FP si no hay reacción, es decir, es w1A. Por otro lado si se considera que no hay reacción wAo=w4A y w1A=w2A=w4A+w3A= w4A+ w4AR=(1+R) w4A, de manera que

Las conversiones X’ se definen sobre la anterior variable de forma que
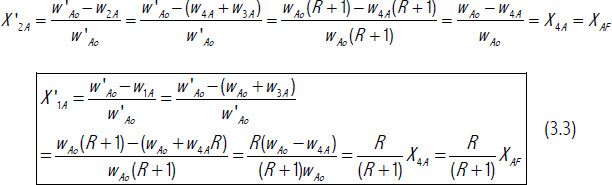
Por tanto, la ecuación de diseño de un RFP con recirculación en función de las variables periféricas es la siguiente

La Figura 3.1 muestra la interpretación gráfica de la ecuación anterior. La integral
 , es decir, el área bajo la curva entre la conversión a la entrada del reactor
, es decir, el área bajo la curva entre la conversión a la entrada del reactor  y la de salida del reactor XAF, es el área de color verde, cuyo valor es
y la de salida del reactor XAF, es el área de color verde, cuyo valor es  .
.Por lo tanto,
 , es el área del rectángulo rayado. El área de la parte azul del rectángulo rayado es R veces el área de la integral I, y el área de la parte gris del rectángulo rayado es equivalente a la integral I. A continuación la Figura 3.2 muestra gráficamente la influencia de la razón de recirculación
, es el área del rectángulo rayado. El área de la parte azul del rectángulo rayado es R veces el área de la integral I, y el área de la parte gris del rectángulo rayado es equivalente a la integral I. A continuación la Figura 3.2 muestra gráficamente la influencia de la razón de recirculación

Si la densidad del medio permanece constante la ecuación de diseño se transforma en
 Razón óptima de recirculación para un volumen mínimo
Razón óptima de recirculación para un volumen mínimoAl observar la variación grafica que produce la razón de recirculación se deduce que existe una razón óptima para la cual el volumen del reactor es mínimo. Dicha razón óptima depende de la forma de la curva cinética y del grado de conversión a alcanzar.
- Si la curva cinética (1/-rA) vs. XA es creciente (reacción irreversible orden n>0) la razón de recirculación óptima es R=0. Por tanto el reactor a emplear es uno de flujo en pistón sin recirculación
- En general, un RFP con recirculación es útil cuando la cinética presenta un máximo, es decir, cuando la curva (1/-rA) vs. XA presenta un mínimo. Esto sucede para fermentaciones microbianas, reacciones adiabáticas exotérmicas y para reacciones autocatalíticas

Ello ocurre cuando las áreas señaladas en la gráfica son iguales. (Demostración matemática Levenspiel, O. Pag 167. Ed Reverté).


Ver también: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18










































No hay comentarios:
Publicar un comentario
Bienvenido a Avibert.
Deja habilitado el acceso a tu perfil o indica un enlace a tu blog o sitio, para que la comunicación sea mas fluida.
Saludos y gracias por comentar!