Reactor de flujo en pistón y reactor discontinuo Diseño de Reactor Ideal (en reacc.multip. simult.)
F.Cunill, M.Iborra, J.Tejero

Los balances de materia en un elemento diferencial de volumen son,

por lo que

lo cual integrado para las condiciones limite de CR0=0 y CAo= CA proporciona las siguientes ecuaciones,

donde la concentración de R queda en función de la de A y de las constantes cinéticas. Por tanto para maximizarla se realiza la derivada de cR respecto a cA y se iguala a cero, lo que proporciona

Sumando los balances de A, R y S se tiene

ecuación que permite conocer cS en función de cR y cA.
Por otro lado, sumando los balances de B, R y 2 veces el de S

se obtiene

ecuación que permite conocer cB en función de cR y cS.
La integración de los balances permitirá finalmente relacionar las concentraciones con el tiempo espacial. La figura siguiente muestra la representación gráfica de la solución.
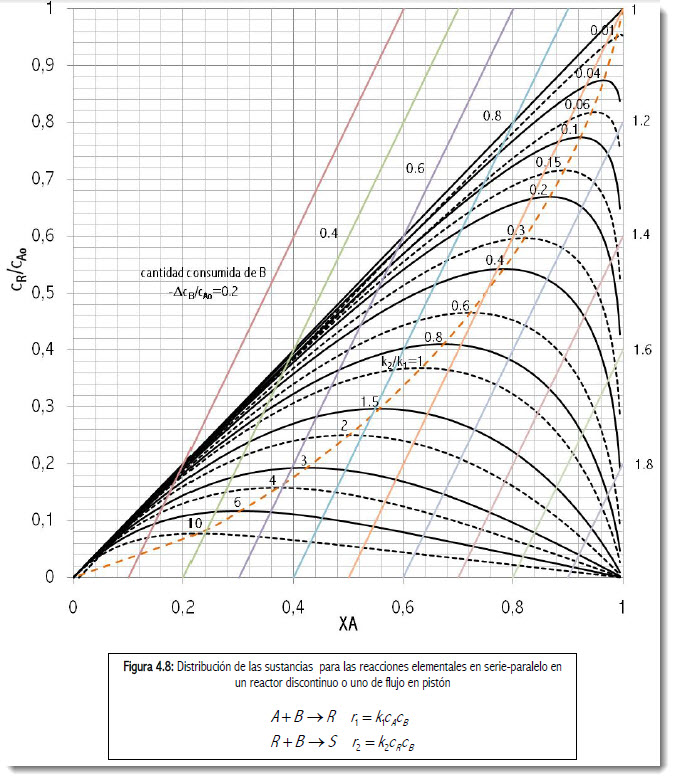
Dada la cinética B influye de igual manera sobre todas las reacciones, por consiguiente en la gráfica anterior se lee la información sobre la distribución de productos igual que en las gráficas de las reacciones en serie.

donde la concentración de R queda en función de la de A y de las constantes cinéticas. Por tanto para maximizarla se realiza la derivada de cR respecto a cA y se iguala a cero, lo que proporciona

Sumando los balances de A, R y S se tiene

ecuación que permite conocer cS en función de cR y cA.
Por otro lado, sumando los balances de B, R y 2 veces el de S
se obtiene
ecuación que permite conocer cB en función de cR y cS.
La integración de los balances permitirá finalmente relacionar las concentraciones con el tiempo espacial. La figura siguiente muestra la representación gráfica de la solución.

Dada la cinética B influye de igual manera sobre todas las reacciones, por consiguiente en la gráfica anterior se lee la información sobre la distribución de productos igual que en las gráficas de las reacciones en serie.
Ver también: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27










































No hay comentarios:
Publicar un comentario
Bienvenido a Avibert.
Deja habilitado el acceso a tu perfil o indica un enlace a tu blog o sitio, para que la comunicación sea mas fluida.
Saludos y gracias por comentar!