Balance de Población Reactores No Ideales
F. Cunill, M.Iborra, J.Tejero, C.Fité
Un tratamiento riguroso requiere conocer los perfiles de concentración, velocidad y temperatura. Dicho conocimiento permitiría describir con todo detalle el comportamiento del reactor. Mediante balances microscópicos y modelos de fenómenos de transporte se podría caracterizar determinadas regiones del reactor y con una posterior integración determinar el comportamiento del reactor. Sólo en determinados casos con una geometría particular y en régimen laminar es posible es posible este tipo de tratamiento. En general no es posible este enfoque por desconocer los perfiles y/o los coeficientes de transporte. En consecuencia, es preciso tratar el problema de otra forma, en concreto mediante métodos estadísticos.
Para obtener información de la macromezcla es suficiente conocer la permanencia de las moléculas dentro del reactor, es decir, la distribución de tiempos de residencia de la corriente de fluido. Dicha información estadística es manejada en los balances de población, introducidos en el campo de los reactores por Danckwerts (1953).
Los conceptos que intervienen en el balance de población aplicado a reactores son:
Es físicamente imposible conocer completamente y con detalle el modelo de flujo del fluido a través del recipiente. Sin embargo, con vistas al diseño, es suficiente en muchos casos conocer el tiempo de permanencia de los elementos de fluido en el recipiente. Aunque el flujo total no presenta variación alguna, no todos los elementos de fluido permanecen el mismo tiempo. La distribución de estos tiempos de residencia se describe mediante las funciones de distribución que se describen a continuación.
Función E(t) o de densidad de distribución de tiempos de residencia (de la corriente de salida)
La función distribución del tiempo de residencia del fluido (DTR) se define, de acuerdo con la teoría de probabilidades, como la frecuencia de distribución de edad de los elementos de fluido que abandonan el recipiente. Tiene las dimensiones de fracción de edad por unidad de tiempo. Así, la fracción de material de la corriente de salida que habiendo entrado a tiempo cero salen del recipiente a un tiempo comprendido entre t1 y t2, es igual a 
Por tanto atendiendo a la definición de E(t) debe cumplirse
Función F(t) o distribución de tiempos de residencia acumulados
La función F(t) representa la fracción volumétrica de fluido que sale del recipiente y ha permanecido en el mismo un tiempo inferior a t. Si la densidad del sistema es constante la fracción volumétrica coincide con la másica.
Según esta definición, la probabilidad de que un elemento de fluido que entró en el reactor a tiempo 0 lo abandone antes de un tiempo t, es justamente F(t). Análogamente, la probabilidad de que lo abandone a un tiempo superior a t es (1-F(t)). De la propia definición también se desprende que
Tiempo medio de residencia, t (ρ=cte)
Se define como tiempo medio de residencia o permanencia de una corriente que circula con un caudal q a través de un recipiente de volumen V a la relación
siempre y cuando se cumplan las siguientes condiciones:
Las funciones de distribución de edad se pueden expresar de forma adimensional, introduciendo en las mismas el tiempo reducido o adimensional θ, definido por
Este cambio en la escala de tiempos tiene las siguientes consecuencias
Los conceptos que intervienen en el balance de población aplicado a reactores son:
- Elemento de fluido: toda porción caracterizable de fluido con propiedades fijas en el recipiente
- Edad: tiempo transcurrido desde que un elemento entra en el sistema hasta el instante considerado
- Tiempo de residencia: tiempo empleado por un elemento de fluido en recorrer el sistema desde la entrada a la salida
Es físicamente imposible conocer completamente y con detalle el modelo de flujo del fluido a través del recipiente. Sin embargo, con vistas al diseño, es suficiente en muchos casos conocer el tiempo de permanencia de los elementos de fluido en el recipiente. Aunque el flujo total no presenta variación alguna, no todos los elementos de fluido permanecen el mismo tiempo. La distribución de estos tiempos de residencia se describe mediante las funciones de distribución que se describen a continuación.
Función E(t) o de densidad de distribución de tiempos de residencia (de la corriente de salida)
Por tanto atendiendo a la definición de E(t) debe cumplirse
Función F(t) o distribución de tiempos de residencia acumulados
La función F(t) representa la fracción volumétrica de fluido que sale del recipiente y ha permanecido en el mismo un tiempo inferior a t. Si la densidad del sistema es constante la fracción volumétrica coincide con la másica.
Según esta definición, la probabilidad de que un elemento de fluido que entró en el reactor a tiempo 0 lo abandone antes de un tiempo t, es justamente F(t). Análogamente, la probabilidad de que lo abandone a un tiempo superior a t es (1-F(t)). De la propia definición también se desprende que
Tiempo medio de residencia, t (ρ=cte)
Se define como tiempo medio de residencia o permanencia de una corriente que circula con un caudal q a través de un recipiente de volumen V a la relación
siempre y cuando se cumplan las siguientes condiciones:
- la densidad de la corriente de fluido no varia a través del reactor
- el sistema es cerrado, es decir, en la entrada y salida del sistema el flujo es en pistón. Ello implica que no hay retromezcla
Las funciones de distribución de edad se pueden expresar de forma adimensional, introduciendo en las mismas el tiempo reducido o adimensional θ, definido por
Este cambio en la escala de tiempos tiene las siguientes consecuencias
si no hay ciertas desviaciones de flujo como zonas muertas o cortocircuitos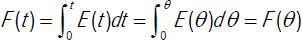
, la función F no varia ya que la fracción de fluido en la corriente de salida que ha permanecido en el recipiente un tiempo comprendido entre t y t+dt o entre θ y θ+dθ es la misma
Ver también: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30
No hay comentarios:
Publicar un comentario
Bienvenido a Avibert.
Deja habilitado el acceso a tu perfil o indica un enlace a tu blog o sitio, para que la comunicación sea mas fluida.
Saludos y gracias por comentar!